Reading rate, IQ, short term memory, and mental speed

The Digit Symbol subtest of the WAIS and WISC intelligence tests is another relatively pure test of mental speed. The so-called concentration test, ‘d2 test’, on fact is an intelligence test, as Westhoff and Kluck (1983) showed empirically: d2 correlates at around r = 0.60 with various intelligence tests in each of the two studies (N1 = 89, N2 = 106). Even generating random numbers contains a component of mental speed when the time for a single choice is limited to a second. Therefore, it correlates moderately with global IQ (Dieminger, 1988; Waddell, Benjamin and Kemp, 1985).

Speed of information processing is hypothesized here to be the common denominator of all the above tests. In samples, correlations between these simple tasks and global IQ vary within a wide range of r = 0.20-0.82. Under favourable conditions (with reliable measures and a full range of intelligence levels among subjects), average correlations of about 0.70 can be expected. For example, in seven representative samples the Number Sequence Test correlated between 0.69 and 0.82 with global intelligence tests (Oswald and Roth, 1978). In summary, we conclude that the overall correlation of speed of information processing with global intelligence is substantial.

Intelligence cannot be claimed to depend on information processing on the basis of correlation coefficients alone. Such correlations merely indicate that performance on the different tasks of intelligence tests has something in common. It could be a complex pattern of strategies at a high cognitive level or, on the contrary, the effect of one simple variable, ubiquitously participating in all performances. The adherents of the Galton paradigm, as Eysenck (1983) called it, prefer the interpretation that a simple parameter speed of information processing determines or constitutes more complex mental achievements. In this sense, mental speed is not only simple but also basic. Besides, it is arguably more intimately connected with biological background than the complex tests which depend essentially on experience (see Figure 1).

In the Galton tradition, we find not only theoretical evidence, concurring from simplicity and closeness to physiological concepts, but also empirical findings promising to accumulate arguments in favour of the assumption that such variables are not governed largely by a complex set of mental processes. Chase, Lyon and Ericsson (1981) and Lyon (1977), as well as Egan (1986), indicated, respectively for memory span and inspection time, that the influence of strategies on some simple variables was relatively small.

Information-processing analyses of cognitive performance

The possibilities which were hardly conceived of by researchers following the Galton and Binet paradigms are (a) the joint total measurement of the stimuli and reactions, and (b) time consumption during one and the same session. Take, for instance, the following item of a conventional intelligence test: ‘Continue the numbers 1 2 4 7 11 16 22 …’. Even when taking into account the time necessary for a solution, nobody can say directly how difficult it was.

The approach of Harwood and Naylor (1969), when determining the so-called MIA (Maximum Rate of Information Acceptance) was very different. Their method of testing enabled the subjects to present themselves a stimulus which remained as long as they kept a finely balanced switch depressed. The stimuli were digits between 1 and 9 or numbers between 1 and 32 presented singly or in groups of two, three, four, or five. By the procedure the time was measured until the signs were perceived by the subjects. The information content of one digit of the repertoire of nine possibilities was 23.17 = 9. That is, 3.17 bits. To recognize one of the 32 possibilities (= 25) was equal to 5 bits.

The MIA of 42 young university students (Naylor, 1968), was 21.4 bits per second (sd = 4.9 bit/s) referring to the repertoire 1-32. The MIA for various adult groups was as follows: for 105 ‘normal’ adults who were 60-69 years old, mean = 14.2 bit/s (sd = 3.4bit/s); for 70-70 years old (N = 67), mean = 12.9 bit/s (sd = 3.7 bit/s); and for the 13 subjects aged 80+, mean = 10.2 bit/s (sd = 3.3 bit/s). With digits (repertoire 1-9) the means were similar (23.5, 15.2, 13.9, and 11.7 bit/s, respectively).

Harwood and Naylor (1969) measured not only the time between stimulus and reaction, but also the amount of stimulus information. This is the precondition for the more striking observation that the results (in bit/s) are numerically equal although the repertoires of signs differ.

The measurement of stimuli and reactions in terms of the information unit (the bit) and physical time will only reveal properties of the subject if the following two prerequisites are fulfilled: (a) the subject processes information in binary decisions, and (b) the information content of the objective repertoire agrees with that of the subjective repertoire. In the latter, the information is more precisely called ‘subjective information’. More generally expressed, the pedagogically oriented information psychology in Germany uses the term ‘subjective information’ to emphasize the information content of a message from a subject’s view. The more novel a message, or the further its distance from existing knowledge, the greater is the subjective information it contains (e.g., Weltner, 1973). As Shands (1959) stated, this seems to be true for both verbal and numeral information processing.

When a repertoire of signs (such as letters, digits, or numbers) is overlearned in normal adults, independently presented signs – for example, the letters in the word ‘uenrd’ in contrast to ‘under’ – have the same objective as subjective information content. Otherwise, many of the experiments mentioned below could not have been successful. The MIA registered by Harwood and Naylor (1969) is in a certain way an example of a complete measurement, being composed of the following three essential parts: (1) stimulus: complexity by subjective information content, presentation time practically zero, and therefore negligible; (2) reaction: complexity (releasing the depressed switch) negligible compared with time of perception (in the case of more than two digits); and (3) time between stimulus and reaction (minus motoric reaction time), measured in ms.

The information amount being processed in a time unit seems to be constant, and independent of the specific information content of a given stimulus (= non-specific). This fact is confirmed by the almost equal absolute average MIA measured by stimuli of different repertoires. The correlations between MIA determined by numbers from 1 to 9 and MIA measured by numbers from 1 to 32 seem to sufficiently high if the high errors of the measurement of digits are taken into account [r(young adults) = 0.36; r(60-69 years old) = 0.68; r(70-79 years old) = 0.68].

Moreover, Harwood and Naylor (1969) conceived of MIA as a fundamental capacity (in the sense of channel capacity) of cerebral data processing, which forms the basis of more complex processes of perception and cognition.

Naylor and Harwood’s experiment was not designed to see whether measured capacity is independent of stimulus mode (visual, auditory, tactile, kinaestethic, etc.). Lehrl and Fischer (see section entitled ‘A general parameter’ below), however, have demonstrated that MIA-related magnitudes are general capabilities.

Probably the key finding in the development of an intelligence theory from the information psychology of perception was the substantial correlation between MIA and intelligence test-scores in normal adults with an approximately representative distribution of IQ [WAIS-full scale: r(digits) = 0.46; r(numbers) = 0.47]. The highest correlations were found with the WAIS subtest ‘Digit symbols’, which is the best indicator of mental speed among all the WAIS subtests [r(digits) = 0.54; r(numbers) = 0.52]. (All correlations were significant at the 0.01 level.) A further indicator of a relation with global IQ is the high MIA of the group who consisted of young university students of presumably high intelligence.

Finally, Harwood and Naylor (1969) emphasized the proximity of MIA to biological variables: According to them, MIA assesses relatively accurately the efficiency of ‘cerebral data processing’. What makes their results especially valuable from the point of view of information psychology is that the data were measured at the level of ratio scales. These features have many advantages for the establishment of relatively simple theories of intelligence, and for practical applications, as will be demonstrated below.

There is one fundamental denominator of all the characteristics of Harwood and Naylor’s (1969) that explains a great deal of the variance and also the correlations with global IQ. It is already contained in MIA. It is the duration of the basic period of central information processing (BIP).

THE INFORMATON PSYCHOLOGICAL PARAMETER ‘BIP’

Currently, there are several conceptualizations of the term speed of (central) information processing, and various corresponding lines of theoretical development. However, here we will delineate the conceptualization in the German-information psychology tradition that is rooted in biological concepts.

The history of the psychological moment: from biology to information psychology

More than a century ago the biologist Von Baer (1864), who is famous as the discoverer of mammalian ova, had the idea that different species in the animal kingdom could be ordered in terms of the speed with which they process changing events. These internal speeds were based on discontinuous psychical units of a certain length (moving like the single frames of a film, as we would say today). He called these units ‘moments’ and presumed that human had six to ten per second, whereas snails of course had distinctly fewer.

Wundt (1874), founder of the first psychological laboratory, took up this idea and determined the human ‘moments’ as having a duration of 1/18 to 1/16 of a second. The biologists Von Uexküll (1928) and Brecher (1932) confirmed these values and claimed their independence of specific sensory modes. Some typical examples of their observations were that 18 acoustic waves per second cannot be distinguished but are heard as a single tone, 18 single pictures of a movie give the impression of a continuous movement, and 18 pinches per second on the same skin area are perceived like one uniform irritation. Similarly, experiments with animals were conducted which led to relatively unequivocal conclusions about their genus-specific moments. So, when snails were touched one to three times per second by a stick, they suddenly moved back. But as soon as they were touched for times or more per second they tried to creep on it, presumably because they perceived it as a fixed object. Therefore, it was concluded that their moments last 1/3 to 1/4 s.

By a similar method, called ‘picture fusion’, Riedel (1966) demonstrated that the moment shortens as children mature. By this method, which is explained in the next section, he investigated children from 7 years (10 moments/s) onward to 15 years (15 moments/s). This latter value is consistent with those of average adults (Lehrl and Fischer, 1988).

A simple measurement of the moment can be conducted by exchanging two pictures like ‘I’ and ‘<’. When increasing the frequency of changes to more than 16 per second, average adults form the impression of a ‘K’. Correspondingly, when slowing down from a high change rate of more than 16 per second to about 14 changes per second the impression arises that there is not one sign but two alternative signs. The mean of the increasing and decreasing procedure is to be taken as characteristics for the moment. For his experiments with children, Riedel used pictures such as two children on a seesaw in two positions (Picture 1: left child up, right down; Picture 2: the reverse). The children had to report their impressions: moving seesaw or two unmoved seesaws forming a cross. It is remarkable that critical flicker fusion (30-50 Hz) has nothing to do with the picture fusion (mean = 15-16 Hz). Theoretically and empirically this was demonstrated by Weidenhammer and Fischer (1985). Their findings are affirmed by the fact that picture fusion is related to intelligence, whereas, according to Jensen’s (1983) results, critical flicker fusion has virtually no correlation with intelligence.

Frank (1959) noticed the numerical agreement between the duration of human moments and the period in which 1 bit of information was processed. He called it the ‘subjective time quant’, and thought its duration in adult humans to be 1/16 s. His concept was supported mainly by two information-theoretical analyses. The first conclusion was drawn from Hick’s (1952) experiments, particularly from the slopes that were obtained when the reaction time was related to binary information content. Frank calculated 1/16 s for the processing of 1 bit of information, presuming that the decisions for the perception of the stimuli were as many as for the reactions because the subjects had to recognize one of a certain number of possible stimuli. In the next step, she/he had to out the correct one of the same number of possible reactions.

The second confirmation came from an experiment by Miller, Bruner and Postman (1954), which was called ‘recognizing letters for different redundancy’. At any one time, they projected tachistoscopically groups of eight letters. The time of presentation varied between several 100 and 1000 ms. The strings of letters had different redundancies. The authors selected four series with redundancies of 0 per cent (e.g. YRULPZOQ), 15 per cent (STANAGOP), 29 per cent (WALLYOF), and 43 per cent (RICANING). At each position of letters the percentage of correct recognitions after a presentation was registered. The period for processing 1 bit of information can be calculated when the time of presentation, the information content of a string, and the percentage of correct responses are known. After the subtraction of the redundancies the curves, which the author published, were almost equal. Using the slope of information increment per time in the range after the first 40 ms, Frank determined the ‘subjective time quant’. It was about 1/16s.

Although the experiment of Miller et al. (1954) was based on language, Frank never doubted the biological nature of the ‘subjective time quant’ because it originated in physiological concepts. The numerical agreement between the duration of the psychological moment, in which there was no inherent necessity to comprehend it as the unit for processing 1 bit of information, and the duration of 1 subjective time quant was striking. Nevertheless, why this connection exists was not clear theoretically.

BIP, the basic determinant of intelligence

Comparing the results of Roth and Frank, Lehrl (1974) presumed that the ‘moment’ during which, according to Frank, 1 bit is processed has to be shorter, the higher the IQ. Empirical investigations to be summarized below have investigated this idea (Lehrl and Erzigkeit, 1976; Lehrl, Erzigkeit and Galster, 1975; Lehrl, Straub and Straub, 1975).

Figure 2. Models of information processing of different repertoires (‘letters’, ‘two stimuli’, ‘two figures’, ‘numbers 1-64’, and number 0-9’). The processes run in binary steps (measured in bits) from top to bottom. Therefore, it needs more decisions to process more extensive repertoires (e.g. letters contain 5 bits of perceptual decision until a reaction may be started) than less extensive ones, such as two stimuli (1 bit until the reaction is possible). On the magnitude that is connected with IQ in this way holds: The higher the IQ, the quicker the processing of 1 bit of information, and the shorter the reaction times.

BIP is the shortest possible time during which a subject can process 1 bit of information. In our account, the processing of information proceeds sequentially, step by step. The necessity to process centrally two bits of information requires two steps, three bits three serial steps, etc. The number of those binary steps is determined by the stimulus itself and the subjectively activated repertoire to cope with this stimulus. Therefore, the adjustment of the subject to the stimulus is extremely important: The same number, for instance 7, has another information content, if the subject expects a digit from 0 to 9 (3.3. bits) or a number between 0 and 31 (5 bits) (see Figure 2).

BIP, which is a capacity, can be measured during the time of about 10 s of maximum effort. The capacity drops. This was discovered while developing adequate measures for serial activities such as reading letters (see below). In the range of about 10 s, there seems to be a series of time intervals of equal duration during each of which 1 bit of information is processed. The maximal information processed during 1 s was called the ‘capacity of information flow to short term store Ck’ (Frank, 1959): in other words, the maximal speed of central information processing during 1 s.

Our first tests for the measurement of Ck, in particular of BIP, were made in a clinic with no funds for basic psychological research. Therefore, the materials were restricted to paper, pencil, and a stop-watch. In addition, we were obliged not to stress the patients, so the tests had to be short and uncomplicated and be of some benefit to bedridden patients. Although under such conditions we could not achieve as sensitive and precise a measure as under laboratory conditions, the important point was to meet the criteria for an information-psychological approach, as outlined above.

With this aim, two tasks (‘letter reading’ and ‘number reading’) were developed. Letter reading, which is described in the Appendix, consists of independent letters that can be read aloud or silently. In the latter, it is established that the subject’s sign for the beginning and the end is the raising and lowering of thumb. The time from the first to the last sound (or sign) is registered. This can be converted to BIP or Ck (see Appendix).

First, we examined whether there were correlations with intelligence. This was investigated in two small samples of adults whose IQs (vocabulary tests) were distributed approximately normally (Lehrl et al., 1975). The one sample (N1 = 18; age 49.9 ± 10.1 years; 13 women, 5 men; IQ: 108.5 ± 12.0) was psychiatrically normal. The other sample (N2 = 34, age= 50.2 ± 11.0; 32 men, 2 women; IQ 97.6 ± 16.3) suffered from endogenous depression. After adjusting for the influence of age, the BIP of N1 correlated with IQ -0.72. In N2 the correlation was –0.54.

These findings were replicated in a more extensive study (Lehrl and Erzigkeit, 1976) with 66 psychiatrically normal adults [age: 39.3 ± 16.1 years; IQ(vocabulary test): 99.3 ± 16.1; r(BIP-IQ) = -0.70].

Thus, the relation with intelligence was confirmed (see Figures 2, 3, and 5). Meanwhile, more empirical studies have been conducted with different samples of psychiatrically normal adults with, in the large, representative IQs as measured by various tests. All such studies support a substantial r(BIP-IQ). A review of these studies carried out by different research groups is presented by Lehrl, Gallwitz, Blaha, and Fischer (1990) (Table 1). The magnitude of the correlation between BIP and intelligence is generally about –0.60.

Table 1. All known studies on correlations between BIP, measured by ‘letter reading’, and traditional intelligence tests

Sample characteristics

Age

Test

mean

total

female

r(BIP-)

MWT-B-IQa

MWT-A-IQb

MWT-A or MWT-B

CFTc

ZVTd

112.5

102.7

108.5

112.4

105.0

99.3

120.6

112.4

105.0

17.3

14.5

12.0

21.8

16.2

16.1

18.6

21.8

16.2

37.1

40.1

46.9

55.1

59.2

39.3

28.0

55.1

59.2

18.9

13.5

10.1

7.2

6.6

16.1

12.0

7.2

6.6

341

105

151

-0.57

-0.61

-0.72

-0.58

-0.60

-0.70

-0.29

-0.80

-0.51e

Note: For further details, see the test manual by Lehrl et al. (1990).

aMehrfachwahl-Wortschatz-Test (Multiple-Choice Vocabulary Test, version B), serves the measurement of the (crystallized) general IQ.

bParallel form of MWT-B, see a.

cCulture-fair-Intelligence test, for (fluid) general IQ.

dZahlen-Verbindungs-Test (Trail-Making test), for (fluid) general IQ.

eA few of these subjects possibly suffered from the beginning of an organic brain syndrome. The remaining correlations are all based on psychiatrically normal subjects.

We have conducted far more studies of psychiatric patients than of normals, but these results are not presented here because they depend on various additional conditions such as type and severeness of the disorder (Blaha, 1980). On the average, the correlations of BIP-IQ obtained with psychiatric patients approach the level of those with normals when the intelligence test is sensitive to acute psychical disorders. This is not the case, for instance, with the vocabulary tests, which are mostly insensitive to cerebral dysfunction. Vocabulary tests are therefore preferred for estimation of ‘premorbid’ IQ. The correlation between BIP and the results of such tests for ‘premorbid’ IQ with psychiatric patients is lower than with normals (Lehrl et al., 1990). Thus, we conclude that BIP indicates the momentary global or general mental efficiency that is usually estimated by global intelligence tests which are highly loaded with the general factor in the Spearman sense.

It is worth mentioning that several of our studies were contrived to find connections between BIP and scores on tests which are variously related to intelligence (Table 2). The ten correlations between BIP and these test scores ranged from 0.52 to 0.82.

Table 2. Results of studies on correlations between BIP, measured by ‘letter reading’, and tests for achievements which are variously related to intelligence

Sample characteristics

Age

Test

mean

total

female

r(BIP-)

Reading words

Reading digits

The same 10 min later

Saying opposites of read words (black ® white, low ® high, etc.)

The same 10 min later

Counting symbols

Reading A for ‘B’ and B for ‘A’ (interference)

108.5

97.6

112.4

105.0

112.4

105.0

12.0

16.3

21.8

16.2

21.8

16.2

46.9

50.2

16 to

55.1

59.2

55.1

59.2

10.1

11.0

7.2

6.6

7.2

6.6

Normals

Depressives

Normals

Normals Normals

0.82

0.54

0.80

0.70

0.61

0.70

0.59

0.55

0.78

0.62

Note: Fur further details,see the test manual by Lehrl et al. (1990)

The backward-masked tasks used in many inspection time measurements give further support for a relationship between BIP and intelligence. The average correlations across those studies between inspection time and IQ are substantial (Irwin, 1984; Longstreth et al., 1986). Even among university students (having restricted variance in intelligence) reliable tachistoscopic estimates of inspection time have been claimed to correlate at around –0.40 with IQ (WAIS-R) (Stough and Nettelbeck, 1989). Furthermore, there are hints of an intimate relation between backward masking and BIP. In the experiment of Longstreth et al. (1986), the efficient intervals, in which the exposed target stimuli had to be identified before it was replaced by a masking stimulus, lasted between 34 and 84 ms. This we know, is the range of the duration of one BIP. In this experiment, the subjects were university students and the subjective information content of each sign was not precisely defined: there were four signs with different probabilities of presentation, and learning stages of the subjects were different. Therefore, the information contents varied between 1 and 2 bits sign. So, the interval contained more than 1, but less than 2 BIP.

It has been argued that BIP is related to more than intelligence when intelligence is understood as a relatively constant state of mental efficiency. Guthke (1986) distinguished between tests of constant state intelligence and dynamic learning intelligence. He viewed status tests as measures of basic components of intelligence or global IQ registering the state of an individual. Learning tests are more dynamic and simulate the complex efficiency claimed to be a component of social intelligence. He favoured the viewpoint that intelligence tests should be learning tests but he could not avoid concluding that (p. 63 ff., translated by the authors): ‘In spite of several theoretical and methodological objections against Frank and Lehrl’s initial premises we confirmed the relations between the so-called basic components “speed of information processing” and “short term storage” and results of state and learning tests. Moreover, we found evidence for even higher correlations between speed of information processing (measured by ZVT by Oswald/Roth [1978] and the reading letters from the KAI/Lehrl) and learning tests than state tests.’

A general parameter

Biologists regard a ‘moment’ as a general property of a species because its absolute length is largely constant and insensitive to different situations and to different methods of operationalization. Correspondingly, the same should be true for the ‘subjective time quant’ and for BIP. However, for the latter individual differences are emphasized as they are in many conventional concepts of information processing. Whereas their generality is indicated by high correlations across different situations and by different procedures, the additional particularity of BIP is that the results of the same subjects should be numerically equal even when different methods are used. That is, a person who is characterized by a BIP of 67 ms by one method of measurement should achieve the same BIP when another procedure is used (allowing for errors of measurement). This presupposes a constant level of motivation.

Table 3. Comparison of results when Ck (bit/s) or BIP (ms) are measured by signs of different physical appearance: letter reading of capitals versus small letters

Sample characteristics

Reading letters

Age

Capitals

Smaller letters

mean

total

female

mean

Ck (bit/s)

Styrene exposed workers

Non-exposed controlls

BIP (ms)

Outpatients

Brain syndrome

Questionable brain syndrome

Without brain syndrome

95.0

98.8

94.7

105.0

112.4

10.9

10.2

12.2

16.2

21.8

39.3

38.1

63.9

59.2

55.1

10.1

10.3

7.9

6.6

7.2

15.3

15.9

16.2

131.8

117.2

100.8

2.3

2.4

3.0

2.8

60.8

81.3

81.2

15.0

15.2

16.1

16.6

134.2

118.3

103.7

2.2

2.4

2.3

2.8

63.0

85.0

92.8

0.84a

0.83b

0.87a

0.85b

0.94a

0.98a

0.99a

Note: For details and data and sources see Lehrl et al. (1990).

a Basic version of ‘letter reading’.

b Parallel version of ‘letter reading’.

Accordingly, we set out to test this prediction. The subtests of ‘letter reading’ were appropriate for such a study because two of the four lines were written in small letters and the other two in capitals. The different physical appearances should not exert an influence on the time of reading, or on CK, or on BIP. This was investigated in five samples of subjects, from which the best value of the two tests with capitals was compared with the best value of the remaining lines [see Table 3; details in Lehrl et al., (1990)]. As expected, different forms of stimuli did not influence the results.

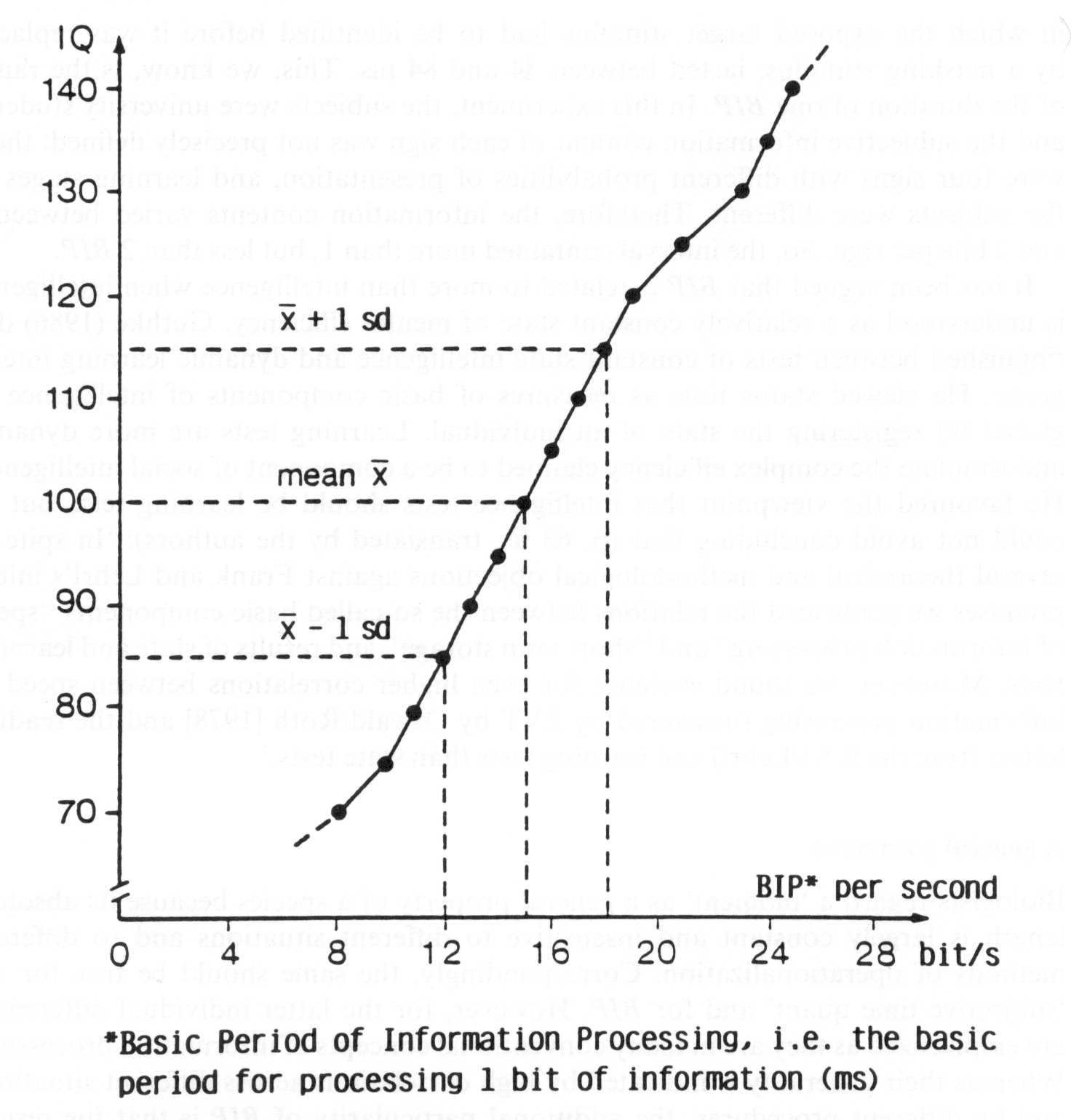
Figure 3. Relationship between the amount of BIP per second and IQ measured by the multiple-choice vocabulary test MWT-B (N=672)

Another study was more ambitious (Lehrl et al., 1975; Lehrl and Fischer, 1988). In addition to capital and small letters, values from 0 to 9 (digits) and 0 to 99 (numbers) were presented. The information content for letters = 4.7 bits, for digits = 3.3. bits, and for numbers (0-99) = 6.6 bits. Responses were both silent and aloud. An example of a line of numbers to be read was: 16 59 81 12 26 41 37 89 96 24. These different procedures were administered to 27 physicians, psychologists, and postgraduates of the Erlangen University (FRG). The median values agreed well. Capital letters aloud = 22 bit/s, silently = 22 bit/s, small letters aloud = 23 bit/s, silently = 23 bit/s, numbers (0-99) silently = 23 bit/s. The average deviation of the individual values across different procedures was 4-5 per cent, i.e. 1 bit/s, and there was no significant deviation. However, this study has some limitations. Speaking numbers aloud usually takes longer than perceiving numbers because they have several syllables. Therefore, the results for reading numbers (0-99) aloud failed to reach the level of about 22 bit/s. The same occurred with reading digits (0-9) silently and aloud. Our preliminary explanation is: The digits extent of repertoire is so small (0-9) that the apperception time is shorter than the time consumption of the reactions which are performed in parallel, such as speaking the digit vocally or subvocally and turning to the next digit.

Another experiment for the investigation of the generality of BIP was conducted using ‘fusion of pictures’, ‘letter reading’, and ‘stimulus reaction time’ (specifically double stimulus minus simple stimulus reaction time). These procedures were administered to 16 workers with lower IQs than the above-mentioned scholars. As expected, their achievements were lower. The medians were: ‘fusion of picture’ = 14 bit/s, ‘letter reading’ = 14 bit/s, and ‘stimulus reaction time’ = 13 bit/s. The correlations of ‘picture fusion’ with ‘letter reading’ = 0.70, with ‘stimulus reaction time’ = 0.69, and the latter with ‘letter reading’ = 0.40. Considering the restricted variance of the values and the high errors of measurement in all of these procedures except ‘letter reading (see section on ‘Facilitating valid measurement’ below), these correlations are remarkable.

Now we discuss the results of additional studies that show approximate numerical agreements using further variables which are assumed to be an expression of BIP (or CK ). However, with the exception of Harwood and Naylor’s (1969) study, these demonstrations are not so convincing because their results concern only the mean of one variable for a certain sample of subjects. Thus, connections between different variables cannot be investigated. Moreover, IQ is often not reported, which is important for the level of BIP measure. As a guide for evaluating their results, university students can be expected to have means of 18 bit/s and more, samples with average education about 15 bit/s, and samples with lower education less than 15 bit/s.

Harwood and Naylor’s (1969) measurement of MIA agree with these statements. In accord with this are estimations of the speed of information processing in adding and multiplying digits by adults. Both the speeds are about 14 bit/s (Lehrl and Fischer, 1988). Applying ‘recognition of letters of different redundancy’ to education students, Frank and Wagner (1982) determined MIA to be 18-19 bit/s.

Wenzel (1961) presented pianists independent musical notes out of a repertoire of 17 possible notes. They were asked to play them as quickly as possible. Wenzel registered the time required and calculated it to be 17.2 bit/s.

In his well-known experiments, Sternberg (1966) presented his subjects with up to two dozen signs from a repertoire. These signs were digits, letters or pictures to be learned by heart. Later, he displayed one sign from the same repertoire and subjects had to indicate as quickly as possible whether they had seen the sign before, either by pressing a button or by responding verbally.

Sternberg’s experiments are comparable to those conducted by Oldfield (1966), who found a linear increment of reaction time [RT (ms)] with the information content (logarithm dualis: ld) of the signs of a repertoire (M): RT (ms) = A + B x ld (M). A symbolizes the intercept and B is the increment of the reaction time when one sign is added to the repertory. This could be the BIP. In reanalyzing a study by Wingfield (1965) who asked his subjects, mostly university students, to search in memory for pictures previously learned, Oldfield obtained the function RT (ms) = 373 + 58 ld (M). Fifty-eight ms for one binary step of search corresponds to 1000/58 ms = 17.2 bit/s. Briggs and Swanson (1969) conducted an experiment confirming Oldfield’s results under the precondition that the repertoire was overlearned.

Other studies in the Sternberg paradigm, however, revealed an increment of reaction times between 37 and 81 ms per scanning one item (e.g. Chapman, McCrary and Chapman, 1981; Ford, Roth, Mohs, Hopkins and Kopell, 1979). Eighty-one ms was found in old adults [mean 80.8 years of age, Ford et al., (1979)] and could be a true value for 1 BIP for such subjects. On the other hand, 37 ms seems to be too short, even for average university students (cf. Table 5). Here confounding effects might have occurred, such as finding out efficient strategies when scanning more than two items, or not scanning exhaustively on positive trials. Confounding effects of this kind are common in reaction time experiments (cf. Longstreth, El-Zahhar and Alcorn, 1985). Therefore, in our measurement of reaction times we limited the procedure to distinguishing between more than two different signs with no more than two responses (press the space key or not).

Studies about event-related potentials in the wake of the Sternberg paradigm seem to reveal a scanning per item even shorter than that indicated by reaction times. According to the survey by Chapman et al. (1981), it varies essentially between 22 and 37 ms. This is too short for one BIP. Fortunately, Ford et al., (1979) published their average results. For their six elderly subjects, ranging in age from 74 to 84 years (mean age = 80.8; WAIS mean raw score = 120, mean IQ = 130), the slope was 27.5 ms per item (digit). It was 27.4 ms per item for their eight young subjects, aged between 20 and 29 years (mean 22.8; WAIS mean raw score = 156; mean IQ = 127). The slopes were averages referring to memory set sizes of 1-4 digits. Positive and negative responses were mixed. When a subject reacts immediately after a coincidence of a probe and a target item, the average holds when scanning 1.5 in two target items (always 1 probe item), 2 in three, and 2.5 in four target items. If negative and positive responses are mixed with equal probability, the decisions are 1 for one target item. An adequate correction would lead to a slope of 35.5 ms/item in the young and 36.6 ms/item in the old subjects. It still seems to be too short to meet the expectations for one BIP (Table 5). However, according to the diagram and the rule-of-thumb calculation, the curves of Ford et al., (1979) show that the slopes from the memory set size of 1-2 target items are the highest – about 40 ms. The slopes from two or three target items are zero or even slightly decreasing and to the end again increasing, but less than form one to two target items. After two target items, strategies seem to be involved. When taking into account the positive responses, the slope for ‘elementary’ scanning amounts to 53.3 ms. This result meets the expectation for one BIP for highly intelligent subjects (cf. Table 5).

Even the control of one-dimensional manual movements towards a target maximally approaches 16 bit/s, respectively 1 bit per 60 ms, as Stier (1969) found in his experiments. The well-known findings by Fitts (1954) and Annett, Colby and Kay (1958) on manual movements only resulted in 11bit/s. But Stier corrected their analyses and obtained about 16 bit/s for these experiments.

By and large, the assumption is supported that BIP is a general parameter. That is, the calculated values are independent of the extent of repertoire of stimuli or reactions, the sense modes or motoric modes mediating the information, and the mode of sign (Figures 2 and 4). Furthermore, it me, Furthermore, it means that BIP, according to the information-psychology position, determines the speed of apprehending (apperception), associating (thinking), comparing, generating information, and scanning from memory. Therefore, the time underlying these various components of information processing is an indicator of the same underlying individual capacity.

A parameter at a ratio or at an absolute scale level?

The measurement by the information unit ‘bit’ and the chronological unit ‘second’ opens the chance to measure BIP (in particular Ck ) at metric levels. These units seem to model the psychological processes adequately. The agreement of numerical results in bit/s obtained in different ways supports the assumption that information is processed in binary steps.

Figure 4. Average values of mental speed expressed as Ck (= BIPs per second). Mean performance of three subject groups in different tasks and studies. (The mixed groups comprise a relatively high percentage of university students).

Moreover, in the measurement of both information units and reaction times, an absolute zero point is given. These two conditions define a ratio level scale. Since an individual is characterized by an absolute number (e.g. 18 bit/s), it is even on an absolute scale.

In order to appreciate this advantage of BIP consider the following example. It would be legitimate to claim that the Ck of a patient 3 h after a surgical operation amounted to 60 per cent of his pre-operative value. In contrast, statements of this kind are not correct for IQ, which is a parameter of frequency in a reference group and not an individual measure.

The absolute point of zero also stresses that BIP is a basic parameter. Therefore, we argue that BIP determines intelligence and not the reverse. This position is supported by the biological nature of BIP as indicated by the methods of its direct psychophysiological measurement by picture fusion or reaction time that was shown above. Subjects with a relatively long moment process little information per unit time and therefore have many difficulties in solving problems in intelligence tests (see Figure 5) or problems in daily life.

Facilitating valid measurement

Because the parameter BIP is a ratio measure, exact values count. A linear transformation of scores, which would be acceptable in correlation studies of IQ, can therefore noticeably distort the results. We have several suggestions for avoiding irregularities of measurement.

Figure 5. Subtest-neutral universality of duration of BIP and empirically confirmed correlations with global IQ. Drawn lines indicate already confirmed relationships. In contrast to traditional information processing tests (with question mark), the subtests recommended here allow BIP to be measured (mean 67 ms for IQ 100).

A general precondition for the measurement of the duration of BIP, as in any other psychological efficiency test, is a well-motivated alert subject. This has to be emphasized because, for instance, resting EEG parameters which are registered in an atmosphere of relaxation are frequently compared with results of psychological efficiency tests. In this case, a good correspondence of electrophysiological and psychological variables cannot be expected.

Subjects should be familiar with the signs whose information has to be processed. Signs that are overlearned are useful, such as letters, numbers or geometrical figures (e.g. circles, crosses, and dots). The same is true for the mode of response. The point is sometimes ignored in stimulus reaction time studies.

The subject has to be prepared for the repertoire of signs (e.g. ‘You will see digits between 0 and 9’, ‘numbers between 0 and 99’, ‘letters’). So that subjective information content corresponds to objective information content. For example, a number from the repertoire 0-9 has 3.3 bits (rounded of, 4 bits). However, within the repertoire 0-99 the information content of the same number is 6.6 bits (rounded off, 7 bits).

When evaluating the raw scores, the information content of the signs should be rounded off because a subject can only perform full binary decisions. Therefore, for one of the digits from 0 to 9 (3.3 bits), 4 full bits should be taken.

The reliability of various procedures for BIP and Ck differs widely. This is illustrated by the retests of 16 patients in a health resort after 24 h [mainly workers suffering from obesity, diabetes, hypertonia, hyperuricemia; nine females; age: 48.5 ± 9.5 years; IQ: 101.3 ± 12.0; more details in Lehrl et al. (1990)]: ‘Reading letters measured by computer’: r(tt) = 0.51; ‘double reaction time minus simple reaction time’: r(tt) = 0.32 (best of each of the ten trials) and r(tt) = 0.13 (second best of each of ten trials); ‘fusion of pictures’: r(tt) = 0.43.

Reading numerals (Weltner, 1987) or reading letters (Table 3 and 4) in paper-and-pencil tests reach reliabilities on the level of well-accepted psychometric tests. Therefore, these are preferred for individual testing or research with small samples.

The most frequently used measurement for Ck (particularly BIP) is letter reading (see Appendix). For about 80 per cent of adults (17-65 years old) it seems to measure a BIP on Ck without distortions. This concerns the middle range between IQ 80 and 120. Here the logarithm of BIP is normally distributed. Additionally, in this range the agreement with other procedures to measure BIP is high (see section entitled ‘A general parameter’). Outside this range, however, distortions may occur which can be caused by the methods and/or sampling errors due to the small number of subjects with extreme values.

Between the IQ 80 and the IQ 120 Ck is distributed normally. Therefore, it is more appropriate for correlations than BIP.

The resulting mean of BIP agrees well with the biological findings (1/15s). Interindividually it varies remarkably in relation to IQ [mean = 67 ms (IQ 100); mean – 1 sd = 83 ms (IQ 85); mean + 1 sd = 56 ms (IQ 115)a; Ck = 15 bit/s, sd = 3.1 bit/s]. Depending on differences in average IQ, there are also characteristic group differences of Ck (or BIP). So, the average value in adults is 15.bit/s (sd = 3.1 bit/s), in medical students 20.2. bit/s, and in the mentally retarded about 9 bit/s or less.

There are several measures that are not adjusted to assess BIP or Ck without distortion because motoric components cannot be controlled. These include: (a) the Reitan Trail Making test; (b) generating random numbers by Licklider’s procedure described by Cherry (1957), as well as Wagenaar’s (1972) procedure; and (c) all tests in which the repertoire of signs changes or refers to different sense modalities. This last category includes one of the Naylor experiments where a combination of numbers and letters had to be selected (Naylor, 1968), and some experiments on complex stimulus reaction times (e.g. Ruchalla et al., 1985).

FURTHER FEATURES OF BIP

BIP is closely related to other indicators of speed of information processing and therefore shares many of their characteristics. For example, Oswald (1981) obtained correlations of between 0.40 and 0.50 between speed of information processing and daily activities, such as personal hygiene and going shopping, of elderly persons. In the same way, many correlations between biochemical and neurophysiological parameters and speed of information processes or global intelligence obtained by Weiss (1984, 1986, 1987) and Eysenck (1979, 1986a, b) are also valid for BIP.

However, new features associated with BIP are even more important. Most of them depend on measurement at a high metric level. As a consequence, comparisons with other human metric parameters are possible.

Integration with biological models of intelligence

Retests after minutes or months and even after more than 1 year (Blaha, Pater and Lehrl, 1978; Lehrl et al., 1990) show that the maximum speed of information processing remains relatively constant (see Table 4). Furthermore, it varies substantially among individuals. Because units of measurement are given, the coefficient of variation by Pearson (CV = 100 x mean/sd) can be assessed. CV of adults = 15 per cent (Lehrl and Fischer, 1988).

Table 4. Reliability coefficients of ‘letter reading’, basic version (if not otherwise marked)

Sample characteristics

Age

Specific reliability

mean

total

female

r(tt)

Split-halfa

Intercorrelation of the four ‘letter reading’ subtests

Retest

8 h later

Retest

14 days later

Retestf 14 months later

95.0

98.8

94.7

105.0

112.4

94.7

105.0

112.4

95.0

98.8

102.7

71.9

10.9

10.2

12.2

16.2

21.8

12.2

16.2

21.8

10.9

10.2

14.5

12.8

39.3

38.1

63.9

59.2

55.1

63.9

59.2

55.1

39.3

38.1

40.1

66.9

65.7

59.8

10.1

10.3

7.9

6.6

7.2

7.9

6.6

7.2

10.1

10.3

13.5

9.4

9.5

9.4

144

182

130

0.91

0.86b

0.95

0.86b

0.96

0.99

0.96-0.98c

0.99c

1.00c

0.86

0.88

0.62

0.94

0.96e

0.89

0.96e

0.70

Immediate retestd

100 female and male university students

between 18 and 28 years

0.81

Note: For detailed data and sources see Lehrl et al. (1990).

a r was calculated between the best of the first two cards and the best of second two cards. Then, according to Spearman-Brown, the correction formula was applied:

r’(tt) = 2 x r(tt)

1 + r(tt)

b Parallel version of ‘letter reading’.

c Calculated on the basis of the Spearman-Brown correction formula for prolongation:

r’(tt) = 4 x r(tt)

1 + 3x r(tt)

d r (original [German] version – Spanish version.

e The values in the line above were taken on the 1st and 15th days. This r(tt) refers to letter reading on the 15th and 29th day, i.e. 14 days later (always basic version).

f r (basic version – parallel version).

Ck or BIP varies more than most biological parameters published by Wechsler (1935). To compare it: body length has a CV = 3-5 per cent and brain weight 8 per cent (Lehrl and Fischer, 1988).

Because BIP is arguably fundamental, biological counterparts can be suggested which reflect numerically comparable processes. In fact, Weiss (1986, 1987) refers to electrophysiological correlations of intelligence to account for the quantitative relations among basic parameters. He even considers the deeper microstructure of time events, and even regards BIP as a unit at a higher level. Although BIP seems to be the elementary unit to process centrally 1 bit of information, the lowest unit in the temporal architecture of mental processes may be the time-quantum T. Geissler (1987) proposed T as an almost universal constant lasting approximately 4.5 ms, in which case BIP would always be an integer multiple of T. We will refrain here from further discussion of more differentiated models of BIP. The combined biophysical, physiological and information psychological conceptions, however, appear to be suitable ways to give a new foundation for the psychology of intelligence.

Experiments with biological and information-psychological parameters registered simultaneously from the same subjects will play an important role in the development of these efforts. Neurophysiological variables, such as evoked potentials, are often used without due consideration of the information content of the stimuli, the alertness and motivation of the subjects, and the beginning of central processes at about 100 ms corresponding to BIP . Lehrl (1980) expects the basic rate of processing 1 bit in averaged evoked potentials to be in the wave after P1 (postcentral: Wernicke’s area and neighbourhood, speech-dominant hemisphere). The reasons are that (a) the latency time between P1 and P2 is the first interval to correlate with global IQ; (b) it corresponds numerically well with 1 BIP; and (c) the simple stimulus reaction time amounts to about 250 ms (minus about 60 ms for the basic decision stimulus yes-no = 190 ms, divided by 2; that is ca. 95 ms for the afferent and 95 ms for the efferent branch.)

Integration with information content of the environment

There is still another important advantage to knowing the individual’s basic capacities for information processing. On the basis of this knowledge it can be assessed whether and how an individual can master the informational aspects of his/her environment. In principle, the assessment succeeds if the informational content and the time of presentation of the messages to be processed are registered. There are several approaches to measure such messages that are understood to be sections of the informational aspects of the human environment. The measurements mainly refer to speech and book reading (Weltner, 1973). For instance, by determination of an individual’s capability of information processing and the information content of a text the necessary time for reading can be predicted. So, for example, an average adult patient (Ck maximally 15-16 bit/s) needs for apperception of each word of drug instructions about 1 s because empirical investigations have shown that the subjective content of each word of average drug instructions amounts to about 16 bits. Because such instructions comprise 600-1000 words, the patient will need 10-17 min for reading only and this without deeper understanding.

In contrast to IQ, which is a parameter solely referring to performances of a subject relative to other subjects, the basic cognitive parameters of an individual, presented here, facilitate quantitative predictions of the individual’s dependence on the information content of the environment. Moreover, quantitative (i.e. metric) models of complicated cognitive parameters and processes can be built on the basis of the parameters presented here. This is particularly important because our society is changing to an information society in which humans’ relatively low capability to process information is being severely taxed. Therefore, Cobarg (1986) argues for a psychologically founded system of strategies to cope with the affluent information, which he calls information hygiene. Mastering the affluent information technically requires more knowledge of psychological moments and the information content of the environment.

FURTHER ELEMENTARY COMPONENTS NECESSARY AND POSSIBLE

BIP correlates with global IQ approximately r = - 0.60. This relation seems to be strong because correlations of global IQ tests such as the WAIS and Raven test are not much higher: mean = 0.65-0.75 (Wolfram, Neumann and Wieczorek, 1986). But here the global IQ was measured by a vocabulary test, which favours verbal, i.e. sequential, binary processes. These, however, organize simultaneously presented information, which is typical for spatial tests such as the Raven test (Das, Kirby and Jarman, 1975). So, they improve the efficiency to master these tasks remarkably. This was shown by Merz (1969) who asked students to verbalize when attempting to solve Raven test tasks. By this approach, their IQ improved 15 points. BIP is the basis unit of analytic and sequential information processing, which seems to be particularly intimately involved in concepts of intelligence. It is still unclear to what degree BIP has to be supplemented by parameters of simultaneous and analogous processes in an attempt to reconstruct conventional concepts of intelligence efficiently.

There is another basic parameter of intelligence and supplement of BIP, which has its own and relatively long history. It is the memory span (or immediate memory, span of apprehension, duration of presence). As two empirical investigations show, BIP and memory span together cover more of global intelligence than does each of them alone. In the one case, r = --0.80 instead of r(BIP -IQ) = -0.70 (N = 66) (Lehrl et al., 1975); in the other, r = -0.67 instead of –0.57 (N = 341) (Lehrl et al., 1990).

After accounting for the errors of measurement of each of the correlated variables, only little residual variance is left over to cover additional aspects of IQ. The question is whether there are any more components to consider for the reconstruction of intelligence. Although for many practical purposes one or two elementary variables may suffice to represent global intelligence, for more complete functional models more variables need to be taken into account. Examples are the flexibility in shifting from one repertoire to signs to another, or control of information processes, or persistence. Unfortunately, these variables can only be measured on a lower scale level than BIP. We can only hope that new ways will be found for measuring such additional variables on a high quantitative level, too.

Much research still needs to be done on the information psychological concept of intelligence presented here. Referring to BIP in particular, the concept and findings may appear too simple in view of the sometimes strikingly inconsistent results (e.g. concerning slope in reaction time studies or slopes in the Sternberg paradigm). We need to enquire whether investigations outside of the information psychological tradition have been designed with the necessary preconditions. However, the results on the basis parameters of information processing demonstrate the possibility of reconstructing the complex and sometimes fuzzy traditional concept of intelligence by means of relatively simple, general, easily measurable and precisely-defined basis variables, which seem to be adequate for an integration with biological models.

ACKNOWLEDGEMENTS

We would like to thank Dr. C. Brand (UK), Dr. V. Weiss (GDR), Dr. S. E. Hampson (USA), and several anonymous reviewers for their comments on earlier drafts of this paper.

REFERENCES

Annett, J., Colby, C. W. and Kay, H. (1958): The measurement of elements in an assembly task – the information output of the human motor system. Quarterly Journal of Experimental Psychology 10: 1-11.

Blaha, L. (1980): Information psychological procedures of measurement within psychiatry. In: Proceedings of the 9th International Congress on Cybernetics, Namur: Association de Cybernetique, pp. 519-527.

Blaha, L., Pater, W. and Lehrl, S. (1978): Neue empirische Untersuchungen zur Zuverlässigkeit und Gültigkeit von Meßverfahren des Kurzspeichers als Intelligenzkorrelat. Grundlagenstudien der Kybernetik und Geisteswissenschaften 19: 11-18.

Brand, C. R. (1984): Intelligence and inspection time: an ontogenetic relationship? In: Turner, C. H. (Ed.), The Biology of Human Intelligence. North Humberside: Natterton, pp. 53-64.

Brecher, G. A. (1932): Die Entstehung und biologische Bedeutung der subjektiven Zeiteinheit – des Moments. Zeitschrift für vergleichende Physiologie 18: 204-234.

Briggs, G. E. and Swanson, J. M. (1969): Retrieval time as a function of memory ensemble size. Quarterly Journal of Experimental Psychology 21: 185-191.

Carena, J. C. (1985): Adaptigo de la inteligentectesto KAI al la hispana lingvoregiono. Grundlagenstudien der Kybernetik und Geisteswissenschaften/Humankybernetik 26: 61-64.

Carlson, J. S. and Jensen, C. M. (1982): Reaction time, movement time, and intelligence: a replication and extension. Intelligence 6: 265-274.

Chapman, R. M., McCrary, J. W. and Chapman, J. A. (1981): Memory processes and evoked potentials. Canadian Journal of Psychology 35: 201-212.

Chase, W. G., Lyon, D. R. and Ericsson, K. A. (1981): Individual differences in memory span. In: Friedman, M. P., Das, J. P. and O’Connor, N. (Eds.), Intelligence and Learning. New York: Plenum, pp. 29-42.

Cherry, C. E. (1957): On Human Communication. 2nd ed., Cambridge, MA: MIT Press.

Cobarg, C. C. (1986): Informationshygiene – Kritische Gedanken zur wachsenden Medienwelt. Geriatrics Pregeriatrics – Rehabilitation 2: 119-132.

Cohn, S. J., Carlton, J. A. S. and Jensen, A. R. (1985): Speed of information processing in academically gifted youth. Personality and individual Differences 6: 621-629.

Das, J. P., Kirby, J. and Jarman, R. F. (1975): Simultaneous and successive syntheses: an alternative model for cognitive abilities. Psychological Bulletin 82: 87-103.

Dieminger, H. (1988): Abhängigkeit der Kreativitätsleistungen erwachsener Patienten von deren Affektivitätsniveau, Intelligenzquotient, Alter und Geschlecht. Diss., Universität Erlangen.

Donders, F. C. (1868): Die Schnelligkeit psychischer Prozesse. Archiv für Anatomie, Physiologie, wissenschaftliche Medizin 6: 657-681.

Egan, V. (1986): Intelligence and inspection time: do high-IQ subjects use cognitive strategies? Personality and individual Differences 7: 695-700.

Eysenck, H. J. (1967): Intelligence assessment: a theoretical and experimental approach. British Journal of Educational Psychology 37: 81-98.

Eysenck, H. J. (1979): The Structure and Measurement of Intelligence. Berlin: Springer.

Eysenck, H. J. (1983): A measure of intelligence. New Scientist 10: 668-669.

Eysenck, H. J. (1986a): Toward a new model of intelligence. Personality and individual Differences 7: 731-736.

Eysenck, H. J. (1986b): The theory of intelligence and the psychophysiology of cognition. In: Sternberg, R. J. (Ed.), Advances in the Psychology of Human Intelligence, Vol. 3. Hillsdale, NJ: Erlbaum, pp. 1-34.

Fitts, P. M. (1954). The information capacity of the human motor system in controlling the amplitude of movement. Journal of Experimental Psychology 47: 381-391.

Ford, J. M., Roth, W. T., Mohs, R. C., Hopkins, W. F. III and Kopell, B. S. (1979): Event-related potentials recorded from young and old adults during a memory retrieval task. Electroencephalography and Clinical Neurophysiology 47: 450-459.

Frank, H. G. (1959): Informationsästhetik – Grundlagenprobleme und erste Anwendungen auf die Mime pure. Waiblingen.

Frank, H. G. und Wagner, H. (1982): Messung der Apperzeptionsgeschwindigkeit mit einem Experimentalfilm. Grundlagenstudien der Kybernetik und Geisteswissenschaften/Humankybernetik 23: 73-79.

Galton, F. (1892): Hereditary Genius: An Inquiry into its Laws and Consequences. London: Macmillan 1892.

Geissler, H.-G. (1987): The temporal architecture of central processing: evidence for a tentative time-quantum model. Psychological Research 49: 99-106.

Grice, G. R. (1955): Discrimination reaction time as a function of anxiety and intelligence. Journal of Abnormal and Social Psychology 50: 71-74.

Guthke, J. (1986): Grundlagenpsychologische Intelligenzforschung und Lerntestkonzept. In: Schaarschmidt, U., Berg, M. and Hänsgen, K.-D. (Eds.), Diagnostik geistiger Leistungen. Berlin: Deutscher Verlag der Wissenschaften, pp. 53-66.

Harwood, E. and Naylor, G. F. K. (1969): Rates and information transfer in elderly subjects. Australian Journal of Psychology 2: 127-136.

Hick, W. (1952): On the rate of gain of information. Quarterly Journal of Experimental Psychology 4: 11-26.

Irwin, R. J. (1984): Inspection time and its relation to intelligence. Intelligence 8: 47-65.

Jenkinson, J. C. (1983): Is speed of information processing related to fluid or to crystallized intelligence. Intelligence 7: 91-106.

Jensen, A. R. (1983): Critical flicker frequency and intelligence. Intelligence 7: 217-225.

Jeske, H., Lehrl, S. and Frank, H. (1982): ‚Faustformeln’ zum IQ. Grundlagenstudien der Kybernetik und Geisteswissenschaften/Humankybernetik 23: 23-27.

Lally, M. and Nettelbeck, J. (1977): Intelligence, reaction time and inspection time. American Journal of Mental Deficiency 82: 273-281.

Lehrl, S. (1974): Subjektives Zeitquant und Intelligenz. Grundlagenstudien der Kybernetik und Geisteswissenschaften 15: 91-96.

Lehrl, S. (1980): Subjektives Zeitquant als missing link zwischen Intelligenzpsychologie und Neurophysiologie. Grundlagenstudien der Kybernetik und Geisteswissenschaften 21: 107-116.

Lehrl, S. and Erzigkeit, H. (1976): Determiniert der Kurzspeicher das allgemeine Intelligenzniveau? Grundlagenstudien der Kybernetik und Geisteswissenschaften 17: 109-119.

Lehrl, S. and Fischer, B. (1988): The basic parameters of human information processing. Personality and individual Differences 9: 883-896.

Lehrl, S., Erzigkeit, H. and Galster, J. V. (1975): Messungen der Apperzeptionsgeschwindigkeit auf dem Absolutskalenniveau. Eine experimentelle Untersuchung. Grundlagenstudien der Kybernetik und Geisteswissenschaften 15: 1-11.

Lehrl, S., Gallwitz, A., Blaha, L. and Fischer, B. (1990): Grundgrößen der Intelligenz. Kurztest KAI und seine Grundlagen. Ebersberg: Vless 1990.

Lehrl, S., Straub, B. and Straub, R. (1975): Informationspsychologische Elementarbausteine der Intelligenz. Grundlagenstudien der Kybernetik und Geisteswissenschaften 16: 41-50.

Leonard, J. A. and Carpenter, A. (1964): On the correlation between a serial choice reaction task and subsequent achievement at typewriting. Ergonomics 7: 197-204.

Longstreth, L. E., El-Zahhar, N. and Alcorn, M. B. (1985): Exception to Hick’s law: explorations with a response duration measure. Journal of Experimental Psychology: General 114: 417-434.

Longstreth, L. E., Walsh, D. A., Alcorn, M. B., Szeszulski, P. A. and Manis, F. R. (1986): Backward masking, IQ, SAT and reaction time: interrelationship and theory. Personality and individual Differences 7: 643-651.

Lyon, D. R. (1977): Individual differences in immediate serial recall: a matter of mnemonics? Cognitive Psychology 9: 403-411.

Merkel, J. (1885): Die zeitlichen Verhältnisse der Willensthätigkeit. Philosophische Studien 2: 73-121.

Merz, F. (1969): Der Einfluß des Verbalisierens auf die Leistung bei Intelligenzaufgaben. Zeitschrift für experimentelle und angewandte Psychologie 16: 114-137.

Miller, G. A., Bruner, J. S. and Postman, L. (1954): Familiarity of letter sequences and tachistoscopic identification. Journal of General Psychology 50: 129-139.

Naylor, G. F. K. (1968): Perception times and rates as a function of the qualitative and quantitative structure of the stimulus. Australian Journal of Psychology 20: 165-172.

Nettelbeck, T. (1987): Inspection time and intelligence. In: Vernon, P. A. (Ed.), Speed of Information Processing and Intelligence. Norwood, NY: Ablex, pp. 295-356.

Oldfield, R. C. (1966): Things, words and the brain. Quarterly Journal of Experimental Psychology 18: 340-353.

Oswald, W. D. (1971): Über Zusammenhänge zwischen Informationsverarbeitungsgeschwindigkeit, Alter und Intelligenzstruktur beim Kartensortieren. Psychologische Rundschau 22: 197-202.

Oswald, W. D. (1981): Das Nürnberger Alters-Inventar NAI als psychometrische Methode der klinischen Pharmakologie. In: Platt, D. (Ed.), Funktionsstörungen des Gehirns im Alter. Stuttgart: Schattauer, pp. 129-136.

Oswald, W. D. and Roth, E. (1978): Der Zahlenverbindungs-Test (ZVT). Handanweisung. Göttingen: Hogrefe.

Reitan, R. M. (1959): Correlations between the Trail Making Test and the Wechsler-Bellevue Scale. Perceptual and Motor Skills 9: 127-130.

Riedel, H. (1966): Untersuchung zur Abhängigkeit des Zeitauflösungsvermögens vom Lebensalter. Grundlagenstudien der Kybernetik und Geisteswissenschaften 7: 65-72.

Roth, E. (1964): Die Geschwindigkeit der Verarbeitung von Informationen und ihr Zusammenhang mit Intelligenz. Zeitschrift für experimentelle und angewandte Psychologie 11: 616-623.

Ruchalla, E., Schalt, E. and Vogel, F. (1985): Relations between mental performance and reaction time: new aspects of an old problem. Intelligence 9: 189-205.

Shands, H. C. (1959): Adaptation and information in psychiatry. Journal of Nervous and Mental Diseases 128: 204-213.

Smith, G. A. and Stanley, G. V. (1980): Clocking g: relating intelligence and measures of timed performance. Intelligence 7: 353-368.

Spiegel, M. L. R. and Bryant, D. (1978): Is speed of processing information related to intelligence and achievement. Journal of Educational Psychology 70: 904-910.

Stabler, J. R. and Dyal, J. K. (1963): Discriminative reaction time as a joint function of manifest anxiety and intelligence. American Journal of Psychiatry 76: 484-487.

Sternberg, S. (1966): High-speed scanning in human memory. Science 153: 652-654.

Stier, F. (1969): Über den Informationsgehalt manueller Zielbewegungen. Kybernetik 5: 209-219.

Stough, C. and Nettelbeck, T. (1989): Inspection time and IQ. The Psychologist 45: 374.

Vernon, P. A. and Jensen, A. R. (1984): Individual and group differences in intelligence and speed of information processing. Personality and individual differences 5: 411-423.

Von Baer, K. E. (1864): Welche Auffassung der lebenden Natur ist die richtige und wie ist diese Auffassung auf die Entomologie anzuwenden? St. Petersburg: Schmitzdorf.

Von Helmholtz, H. I. F. (1887): Zählen und Messen erkenntnistheoretisch betrachtet. In: Philosophische Aufsätze. Leipzig: Fues, pp. 1-28.

Von Uexküll, J. (1928): Theoretische Biologie. 2nd ed. Berlin: Springer.

Waddell,P. A., Benjamin, L. and Kemp, S. (1985): Random number generation by normal subjects. Perceptual and Motor Skills 61: 710.

Wagenaar, W. A. (1972): Generation of random numbers by human subjects: a critical survey of literature. Psychological Bulletin 77: 65-72.

Wechsler, D. (1935): The Range of Human Capacities. London: Bailliere.

Weidenhammer, W. and Fischer, B. (1985): Flimmerverschmelzungsfrequenz und Subjektives Zeitquant – sind sie unabhängige Größen? Grundlagenstudien der Kybernetik und Geisteswissenschaften/Humankybernetik 26: 51-60.

Weiss, V. (1984): Psychometric intelligence correlates with interindividual different rates of lipid peroxidation. Biomedica and Biochimica Acta 43: 755-763. – see update http://www.v-weiss.de/majgenes.html and http://www.v-weiss.de/intellig.html

Weiss, V. (1986): From memory span and mental speed toward the quantum mechanics of intelligence. Personality and individual Differences 7: 737-749. – see update http://www.v-weiss.de/publ9-e.html

Weiss, V. (1987): The quantum mechanics of EEG-brain dynamics and short term memory. Biologisches Zentralblatt 106: 401-408. – see update http://www.v-weiss.de/chaos.html

Weltner, K. (1987): The Measurement of Verbal Information in Psychology and Education. Heidelberg: Springer.

Weltner, K. (1987): Messung des Zeitbedarfs für elementare Verknüpfungsoperationen. Grundlagenstudien der Kybernetik und Geisteswissenschaften/Humankybernetik 28: 37-45.

Wenzel, F. (1961): Über die Erkennungszeit beim Lesen. Kybernetik 1: 32-36.

Westhoff, K. and Kluck, M.-L. (1983): Zusammenhang zwischen Intelligenz und Konzentration. Diagnostica 23: 310-319.

Wingfield, A. (1965): The identification and naming of objects. Diss., Oxford.

Wolfram, H., Neumann, J. and Wieczorek, V. (1986): Psychologische Leistungstests in der Neurologie und Psychiatrie. Leipzig: Thieme.

Wundt, W. (1874): Grundzüge der Physiologischen Psychologie. Leipzig: Engelmann.

APPENDIX

How to administer the letter-reading task and derive a testee’s BIP

There are several measures for BIP and Ck and – via these magnitudes – for the IQ. Among all the administered measures ‘Letter reading’ was developed as a test because it proved to be sufficiently objective, reliable (Tables 3 and 4 ), valid (Tables 1, 2, 3, and 5; Figure 3), and practicable (Table 4). Its acceptance by testees is high.

Letter reading consists of four cards (each 15 x 21 cm). In the middle of each card is a line of 20 independent letters, having phonetically only one syllable. The size of each line is 0.7 x 18 cm. The first card in the German basic version of letter-reading follows. This and all other cards may also fit the English administration.

w n r z t r f e p k b v d s n i l d m r

The subject is simply asked to read a series of mixed up letters in an undertone as quickly as possible. The he or she obtains the first card with the back upwards. As soon as the testee has reversed the card and begins to speak, the stopwatch is started. The time from the first to the last spoken letter is measured. It should be documented in tenths of a second, e.g. 7.3 s.

If the subject has repeated one or more letters or has delayed for other reasons, he or she is asked to continue even if there are mistakes. Then the next of three similar cards with other letters is given. The corresponding German versions are

I P L Z M B E O A E H I O A Z T L E A V

m j z t f r d s i h d o l t k g d e r i

E C X S B T L K E O G F D E A V I M H P

The total procedure takes about 1-3 min. Only the best time counts. When evaluating the raw scores it must be remembered that a subject can only perform full binary decisions. Therefore, the recognition of a letter out of the repertoire of 27 letters, which theoretically has an information content of 4.7 bits (27 = 24.7), needs five binary decisions. Since each letter contains 5 bits of information, the 20 letters contain 100 bits. This is divided by the time of reading to obtain the amount of information processed in a second Ck (bit/s). For example, if the best time of a testee is 7.3 s, then Ck = 100/7.3 (bit/s) = 13.7 bit/s. 1000 ms/Ck equals the BIP (ms). In this example, BIP = 137 ms (and likewise, the ‘psychological moment’).

By standardizing ‘letter reading’ on adults, normative data are available for BIP and Ck (Table 5). By Table 5 an additional allocation to IQ is also possible.

Table 5. Normative data of duration of basic period of information processing (BIP) and mental speed Ck measured by the test ‘Letter reading’
Percentile	IQ	1 BIP(ms)	Ck (bit/s)
99.8	140	-41	25
99.7	135	-42	24
98.8	130	43-47	23
96.5	125	48-49	21
93.0	120	50-54	19
86.0	115	-55	18
75.0	110	56-57	17
59.2	105	58-63	16
50.0	100	64-68	15
40.8	95	69-71	14
25.0	90	72-78	13
16.0	85	79-87	12
7.0	80	88-93	11
3.5	75	94-124	9
1.2	70	125-	-8

Although an exhaustive representative inquiry is still lacking, there are indirect estimates of representative values: the parameter BIP (respectively Ck) was measured together with scores on a vocabulary intelligence test which had been standardized on 1952 representative Western German adults in 1974 [for further details see Lehrl et al., (1990)] . The sample consisted of 672 adults (310 females; age: 42.7 ± 21.1 years; IQ 105.6 ± 21.7 years). Within the range of 17-65 years no relevant relation with age was noticed.

Subjects in IQ intervals of 5 points (68-72, 73-77, 78-82, 83.87, etc.) were aggregated and their medians in BIP and Ck calculated. The results were the norms given in Table 5 and the regression lines in Figure 3. Because the connections are linear in the interval from IQ 80 to IQ 120, Jeske, Lehrl and Frank (1982) suggested the following rule of thumb for a quick determination of IQ. IQ = 5 Ck (bit/s) + 25, valid for 11 < Ck < 19, i.e. 80 < IQ < 120.

As an estimate of the scatter, the standard deviation of Ck was determined for the values. which are allocated to the (representative) IQ 115 and IQ 85. The resulting difference was divided by 2. The result is mean (Ck) = 15.0 bit/s; sd = 3.1 bit7s. BIP : mean = 66.7 ms; sd = 19 ms.

The normative data in Table 5 are also valid for the parallel version of Letter-reading, which consists of the lines

d f z k v b r x p l y t a s n d c o g h

L P H M O T V F R G S X E B A K M I D Z

n z k f v s c u l t p m a g x i r y b d

V T B U R K Z F C D P L M S E N I X O Y

There are virtually no systematic retest effects, especially if the parallel version is applied and/or if the interval between two measurements is large (cf. Lehrl et al., 1990).

Findings from Spanish speakers provide some evidence that the norms are valid for people from different language areas (Carena, 1985). For Spanish, letters were omitted which are spoke with more than one syllable (e.g. ‘w’), because in these cases speaking lasts longer than perceiving and thus determines the registered time. Normally, as has been shown (Lehrl et al., 1990), recognizing the new letter already begins while the previously perceived letter is spoken, indicating a parallel process.

Home